1 1 4 In Half
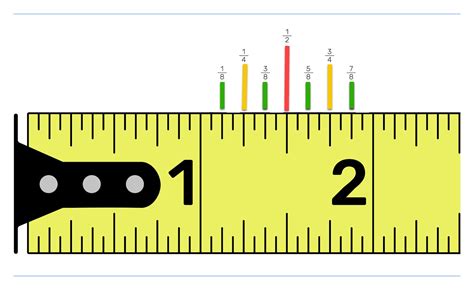
To calculate 1 1 4 in half, we first need to understand the mixed number 1 1 4. This mixed number represents one whole, one half, and one quarter. To find half of 1 1 4, we'll convert the mixed number into an improper fraction or decimal for easier calculation.
Conversion to Improper Fraction

First, let’s convert 1 1 4 into an improper fraction. The whole number part is 1, the half is 1⁄2, and the quarter is 1⁄4. To add these together, we find a common denominator, which is 4. So, 1 whole is 4⁄4, 1⁄2 is 2⁄4, and 1⁄4 remains the same. Adding these gives us 4⁄4 + 2⁄4 + 1⁄4 = 7⁄4.
Calculating Half of 7⁄4
To find half of 7⁄4, we multiply 7⁄4 by 1⁄2. Multiplying fractions involves multiplying the numerators together to get the new numerator and multiplying the denominators together to get the new denominator. So, (7⁄4) * (1⁄2) = (7*1)/(4*2) = 7⁄8.
| Mixed Number | Improper Fraction | Half Calculation |
|---|---|---|
| 1 1 4 | 7/4 | 7/4 * 1/2 = 7/8 |

The result of calculating half of 1 1 4 is 7/8. This demonstrates how to work with mixed numbers and fractions to perform basic arithmetic operations.
Key Points
- Understanding mixed numbers and their conversion to improper fractions simplifies arithmetic operations.
- Converting 1 1 4 to an improper fraction yields 7/4.
- Calculating half of 7/4 involves multiplying by 1/2, resulting in 7/8.
- Working with fractions and mixed numbers requires finding common denominators for addition and understanding multiplication and division principles.
- Practice with different mixed numbers and fractions enhances proficiency in handling various arithmetic operations.
Applying Fractional Arithmetic in Real-World Scenarios

Fractional arithmetic, such as calculating halves or quarters of quantities, is crucial in numerous real-world applications, including cooking, carpentry, and financial planning. Understanding how to convert between mixed numbers and improper fractions and perform operations like multiplication and division by fractions enables individuals to tackle a wide range of problems with precision.
Practical Examples and Applications
In cooking, a recipe might call for 1 1 4 cups of flour, and you need to make half the recipe. Knowing that half of 1 1 4 cups is 7⁄8 cups allows you to accurately measure ingredients. Similarly, in carpentry, calculating exact measurements is critical for fitting parts together perfectly, and being able to work with fractions is essential for success.
Mastering fractional arithmetic not only aids in academic and professional pursuits but also in everyday life, where measurements and quantities often need to be adjusted or calculated with precision.
What is the importance of converting mixed numbers to improper fractions in arithmetic operations?
+Converting mixed numbers to improper fractions simplifies arithmetic operations by allowing for uniform treatment of the quantities involved. It facilitates addition, subtraction, multiplication, and division by providing a common format for the numbers.
How does understanding fractional arithmetic benefit real-world applications?
+Understanding fractional arithmetic is beneficial in various real-world applications, including cooking, carpentry, and financial planning, by enabling precise calculations and measurements. This proficiency is crucial for achieving desired outcomes and avoiding errors in these fields.
What is the process for finding half of a mixed number like 1 1 4?
+To find half of a mixed number like 1 1 4, first convert the mixed number into an improper fraction. Then, multiply this improper fraction by 1⁄2 to find the half. For 1 1 4, which converts to 7⁄4, multiplying by 1⁄2 gives 7⁄8.



