39Cm In Inches
To convert 39 centimeters (cm) to inches, we use the conversion factor where 1 inch is equal to 2.54 centimeters.
Given: - 1 inch = 2.54 cm
We want to convert 39 cm to inches.
Calculation: - 39 cm / 2.54 cm/inch = 15.35433 inches
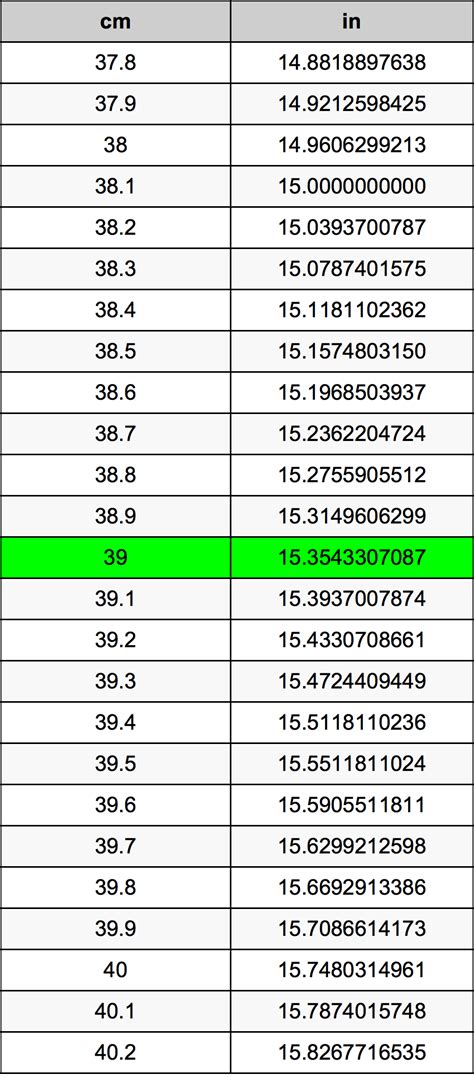
Rounded to two decimal places, 39 cm is approximately 15.35 inches.
Here’s a simple conversion table for reference:
| Centimeters | Inches |
|---|---|
| 30 cm | 11.81 inches |
| 35 cm | 13.78 inches |
| 39 cm | 15.35 inches |
| 40 cm | 15.75 inches |

Keep in mind, this conversion is based on the exact conversion rate of 1 inch = 2.54 cm. For everyday purposes, the approximation is usually sufficient, but for precise measurements, especially in scientific or technical applications, the exact conversion factor should be used.
Conversion Formula:
- inches = cm / 2.54
Using this formula, you can easily convert any measurement in centimeters to inches. Just replace “cm” with your measurement in centimeters.
Key Points:
- 1 inch is equivalent to 2.54 centimeters.
- To convert cm to inches, divide the measurement in cm by 2.54.
- For precise measurements, always use the exact conversion factor.
- Conversion tables can be useful for quick references but may not provide exact values for all measurements.
FAQ:
How do I convert centimeters to inches?
+To convert centimeters to inches, divide your measurement in centimeters by 2.54. For example, to convert 39 cm to inches, you calculate 39 / 2.54.
Is there a simpler way to remember the conversion?
+While there isn't a simpler mathematical formula, you can memorize common conversions (like 1 inch = 2.54 cm) or use a conversion chart for quick references.
Why is accurate conversion important?
+Accurate conversion is crucial in fields like science, engineering, and construction where precise measurements are necessary. Small discrepancies can lead to significant errors in final products or outcomes.
In conclusion, converting 39 cm to inches involves a simple division by 2.54, yielding approximately 15.35 inches. Understanding and applying this conversion accurately is essential across various disciplines for ensuring precision and avoiding potential errors.



