Center Of Mass

The concept of Center of Mass, also known as the Center of Gravity, is a fundamental principle in physics and engineering that describes the point where the entire mass of an object can be considered to be concentrated. This point is crucial in understanding the behavior of objects under the influence of external forces, such as gravity, and is essential in designing and analyzing various systems, from simple pendulums to complex structures like buildings and bridges. In this article, we will delve into the definition, calculation, and application of the Center of Mass, exploring its significance in different fields and providing insights into its practical implications.
Key Points
- The Center of Mass is the point where the entire mass of an object can be considered to be concentrated.
- The calculation of the Center of Mass involves integrating the mass elements of an object over its volume.
- The Center of Mass is crucial in understanding the stability and balance of objects under the influence of external forces.
- Applications of the Center of Mass can be found in various fields, including physics, engineering, and architecture.
- Understanding the Center of Mass is essential for designing and analyzing systems, from simple mechanisms to complex structures.
Definition and Calculation of Center of Mass

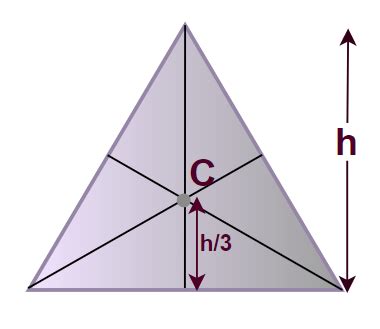
The Center of Mass of an object is defined as the point where the entire mass of the object can be considered to be concentrated. Mathematically, it can be calculated using the formula: x = ∫xdm / ∫dm, where x is the position of the Center of Mass, and dm is the mass element of the object. This formula involves integrating the mass elements of the object over its volume, taking into account the density distribution of the object. For objects with a uniform density, the Center of Mass coincides with the geometric center of the object.
Center of Mass in Different Coordinate Systems
In different coordinate systems, such as Cartesian, cylindrical, or spherical coordinates, the calculation of the Center of Mass requires modifications to the formula. For example, in Cartesian coordinates, the Center of Mass can be calculated using the formula: x = ∫xdm / ∫dm, y = ∫ydm / ∫dm, and z = ∫zdm / ∫dm. Understanding the Center of Mass in different coordinate systems is essential for analyzing and designing systems that involve complex geometries and motions.
| Coordinate System | Center of Mass Formula |
|---|---|
| Cartesian | x = ∫xdm / ∫dm, y = ∫ydm / ∫dm, z = ∫zdm / ∫dm |
| Cylindrical | r = ∫rdm / ∫dm, θ = ∫θdm / ∫dm, z = ∫zdm / ∫dm |
| Spherical | r = ∫rdm / ∫dm, θ = ∫θdm / ∫dm, φ = ∫φdm / ∫dm |
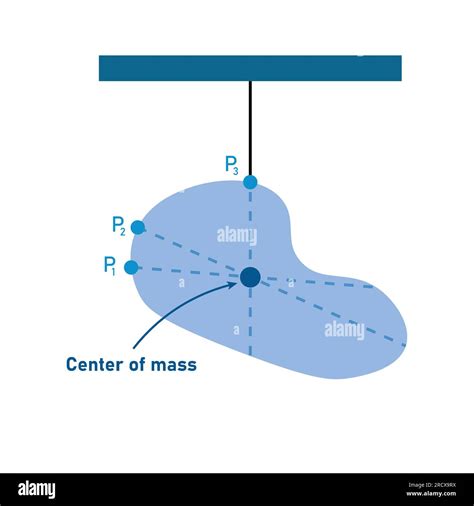
Applications of Center of Mass
The concept of Center of Mass has numerous applications in various fields, including physics, engineering, and architecture. In physics, the Center of Mass is used to describe the motion of objects under the influence of external forces, such as gravity. In engineering, the Center of Mass is essential in designing and analyzing systems, from simple mechanisms to complex structures like buildings and bridges. Architects use the Center of Mass to ensure the stability and balance of buildings, taking into account factors like wind and seismic loads.
Stability and Balance
The Center of Mass plays a crucial role in determining the stability and balance of objects. When the Center of Mass is located within the base of support, the object is stable and will not tip over. However, when the Center of Mass is located outside the base of support, the object is unstable and may tip over. Understanding the Center of Mass is essential for designing and analyzing systems that involve complex geometries and motions, ensuring the safety and efficiency of the system.
In conclusion, the concept of Center of Mass is a fundamental principle in physics and engineering that describes the point where the entire mass of an object can be considered to be concentrated. Understanding the Center of Mass is essential for designing and analyzing systems, from simple mechanisms to complex structures like buildings and bridges. By calculating the Center of Mass, engineers and physicists can predict the stability and balance of objects, ensuring the safety and efficiency of systems.
What is the Center of Mass, and why is it important?
+The Center of Mass is the point where the entire mass of an object can be considered to be concentrated. It is essential in understanding the behavior of objects under the influence of external forces, such as gravity, and is crucial in designing and analyzing systems.
How is the Center of Mass calculated?
+The Center of Mass can be calculated using the formula: x = ∫xdm / ∫dm, where x is the position of the Center of Mass, and dm is the mass element of the object. This formula involves integrating the mass elements of the object over its volume, taking into account the density distribution of the object.
What are the applications of the Center of Mass?
+The concept of Center of Mass has numerous applications in various fields, including physics, engineering, and architecture. It is used to describe the motion of objects under the influence of external forces, design and analyze systems, and ensure the stability and balance of objects.



