Consecutive Interior Angles
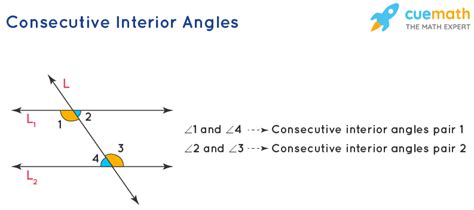
Consecutive interior angles are a fundamental concept in geometry, particularly in the study of parallel lines and transversals. To understand the concept of consecutive interior angles, it’s essential to establish a foundational knowledge of the related terminology and principles.
When two parallel lines are intersected by a transversal, the angles formed can be categorized based on their positions relative to the transversal and the parallel lines. The interior angles are those angles that lie within the two parallel lines. Consecutive interior angles, specifically, are interior angles that are on the same side of the transversal and share a common vertex.
Definition and Properties

Consecutive interior angles are defined as the interior angles that are adjacent to each other, sharing a common vertex, and are on the same side of the transversal. A key property of consecutive interior angles is that they are supplementary, meaning their sum is always 180 degrees. This property is a direct result of the parallel lines being intersected by the transversal, creating corresponding angles that are equal and supplementary angles that sum to 180 degrees.
For instance, in a scenario where a transversal intersects two parallel lines, forming two consecutive interior angles, the measure of one angle can be determined if the measure of the other angle is known. Given that the sum of these angles is 180 degrees, one can calculate the measure of the unknown angle by subtracting the known angle's measure from 180 degrees.
Key Points
- Consecutive interior angles are supplementary, summing to 180 degrees.
- They are formed when a transversal intersects two parallel lines.
- The angles share a common vertex and are on the same side of the transversal.
- Understanding consecutive interior angles is crucial for solving problems involving parallel lines and transversals.
- These angles play a significant role in geometric proofs and theorems related to parallel lines.
Applications in Geometry
Consecutive interior angles have numerous applications in geometry, particularly in the context of parallel lines and transversals. They are instrumental in proving theorems related to parallel lines, such as the converse of the corresponding angles postulate, which states that if two lines are cut by a transversal and corresponding angles are congruent, then the lines are parallel.
A strong grasp of consecutive interior angles is also essential for solving problems involving the properties of parallel lines, including determining angle measures, proving line relationships, and applying geometric principles to real-world scenarios.
| Property | Description |
|---|---|
| Supplementary | Consecutive interior angles sum to 180 degrees. |
| Corresponding Angles | Angles in the same relative position in each intersection are equal. |
| Alternate Interior Angles | Angles on opposite sides of the transversal and inside the two lines are equal. |

Real-World Applications

The concept of consecutive interior angles extends beyond the realm of abstract geometry, having practical applications in various fields such as architecture, engineering, and design. Understanding the properties of consecutive interior angles is crucial for designing structures, analyzing spatial relationships, and solving problems that involve parallel lines and transversals.
For example, in architecture, the principles of consecutive interior angles can be applied to the design of buildings, ensuring that structures are stable and aesthetically pleasing. Engineers also rely on these principles to design and analyze systems involving parallel components, such as railway tracks or highway lanes.
Solving Problems Involving Consecutive Interior Angles
When solving problems involving consecutive interior angles, it’s essential to apply the properties and theorems related to parallel lines and transversals. This includes identifying corresponding angles, alternate interior angles, and using the fact that consecutive interior angles are supplementary to find unknown angle measures.
A systematic approach to problem-solving, which includes drawing diagrams, identifying known angles, and applying relevant theorems, is critical for success. Additionally, recognizing the relationships between different types of angles formed by parallel lines and transversals can significantly simplify the solution process.
What is the sum of consecutive interior angles formed by a transversal intersecting two parallel lines?
+The sum of consecutive interior angles is always 180 degrees, as they are supplementary.
How are consecutive interior angles used in real-world applications?
+Consecutive interior angles are applied in architecture, engineering, and design to ensure structural stability and aesthetic appeal, and to solve problems involving parallel components.
What is the significance of understanding consecutive interior angles in geometry?
+Understanding consecutive interior angles is crucial for proving theorems related to parallel lines, solving problems involving parallel lines and transversals, and applying geometric principles to real-world scenarios.
In conclusion, consecutive interior angles are a fundamental concept in geometry, with properties and applications that are both theoretically profound and practically relevant. By grasping the definition, properties, and real-world applications of consecutive interior angles, individuals can deepen their understanding of geometric principles and enhance their problem-solving capabilities in mathematics and beyond.



