How To Find The Inverse Of A Function

Finding the inverse of a function is a fundamental concept in mathematics, particularly in algebra and calculus. The inverse of a function essentially reverses the operation of the original function, allowing us to solve for the input value when the output value is known. In this article, we will delve into the process of finding the inverse of a function, exploring the steps involved, and examining the properties and applications of inverse functions.
Introduction to Inverse Functions
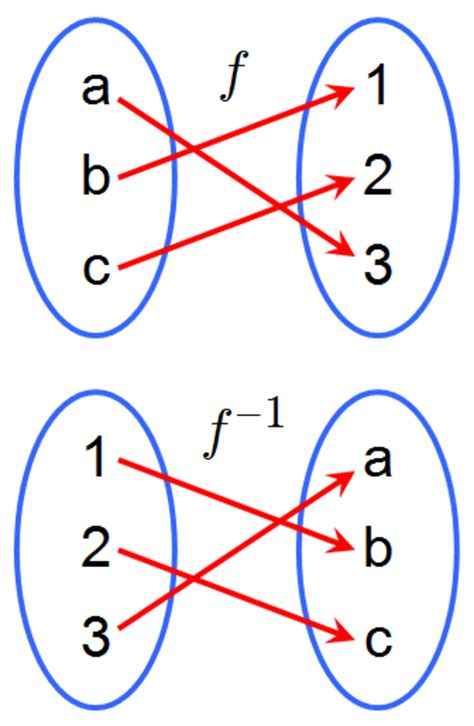
To begin with, let’s define what an inverse function is. Given a function f(x), its inverse is denoted as f^(-1)(x) and is defined as a function that undoes the action of the original function. In other words, if f(x) maps an input x to an output y, then f^(-1)(y) maps the input y back to the original input x. This relationship can be expressed as f(f^(-1)(x)) = x and f^(-1)(f(x)) = x.
Steps to Find the Inverse of a Function

Finding the inverse of a function involves a series of steps:
- Write the function as y = f(x): Start by expressing the given function in terms of y.
- Swap the variables x and y: Interchange the x and y variables to begin solving for the inverse function.
- Solve for y: Rearrange the equation to isolate y, which will give you the inverse function f^(-1)(x).
- Check for one-to-one correspondence: Ensure that the original function is one-to-one, meaning that each output value corresponds to exactly one input value. If the function is not one-to-one, it may not have an inverse.
Example: Finding the Inverse of a Simple Function
Consider the function f(x) = 2x + 1. To find its inverse:
- Write the function as y = 2x + 1.
- Swap the variables: x = 2y + 1.
- Solve for y: x - 1 = 2y, then (x - 1)/2 = y.
- The inverse function is f^(-1)(x) = (x - 1)/2.
Properties of Inverse Functions
Inverse functions have several important properties:
- Domain and range: The domain of the inverse function is the range of the original function, and vice versa.
- Composition: The composition of a function and its inverse yields the identity function, i.e., f(f^(-1)(x)) = x and f^(-1)(f(x)) = x.
- Graphical representation: The graph of an inverse function is the reflection of the graph of the original function across the line y = x.
Applications of Inverse Functions
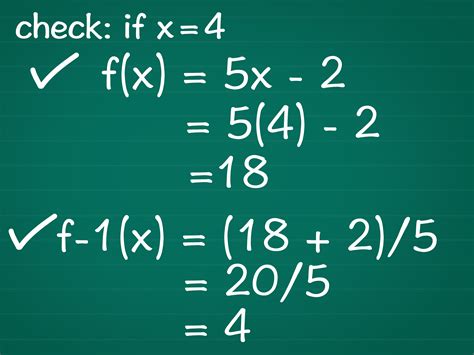
Inverse functions are crucial in various mathematical and real-world applications:
- Solving equations: Inverse functions can be used to solve equations where the variable is part of the argument of the function.
- Calculus: Inverse functions play a significant role in calculus, particularly in the study of differentiation and integration.
- Data analysis: Inverse functions can help in understanding and analyzing data, especially in cases where the relationship between variables is not straightforward.
Key Points
- The inverse of a function undoes the action of the original function, mapping the output back to the input.
- Finding the inverse involves swapping x and y, solving for y, and ensuring one-to-one correspondence.
- Inverse functions have unique properties, including specific domain and range relationships and compositional identities.
- Applications of inverse functions are diverse, ranging from solving equations and calculus to data analysis and more.
- Understanding inverse functions is essential for advanced mathematical studies and practical problem-solving.
Advanced Concepts and Considerations
In more advanced contexts, the concept of inverse functions extends to include:
- Partial inverses: For functions that are not one-to-one, partial inverses can be defined over specific intervals where the function is injective.
- Inverse trigonometric functions: These are used to solve triangles and are essential in trigonometry and its applications.
- Inverse matrix functions: In linear algebra, the inverse of a matrix (if it exists) can be used to solve systems of linear equations.
Conclusion
Finding the inverse of a function is a fundamental skill that underpins many mathematical and real-world applications. By understanding how to find and apply inverse functions, individuals can deepen their insight into mathematical relationships and solve a wide range of problems. Whether in algebra, calculus, or data analysis, the concept of inverse functions is a powerful tool that offers a unique perspective on the relationships between variables.
Natural Applications and Further Considerations
In natural applications, inverse functions can be seen in physics, engineering, economics, and more. For instance, in physics, the inverse function can help in understanding the relationship between distance and time when the acceleration is not constant. In economics, inverse functions can model the supply and demand curves, showing how changes in one variable affect the other.
Practical Examples of Inverse Functions in Real-World Scenarios
Consider a company that produces goods based on demand. The demand function can be seen as the inverse of the supply function, where the demand is inversely related to the price. Understanding this relationship can help the company in setting prices and production levels. Similarly, in engineering, inverse functions can be used in the design of electronic circuits, where the output voltage is a function of the input voltage.
| Function Type | Original Function | Inverse Function |
|---|---|---|
| Linear | f(x) = 2x + 1 | f^(-1)(x) = (x - 1)/2 |
| Quadratic | f(x) = x^2 | f^(-1)(x) = ±√x |
| Exponential | f(x) = e^x | f^(-1)(x) = ln(x) |

What is the purpose of finding the inverse of a function?
+The purpose of finding the inverse of a function is to solve for the input value when the output value is known. It essentially reverses the operation of the original function.
How do you determine if a function has an inverse?
+A function has an inverse if it is one-to-one, meaning that each output value corresponds to exactly one input value. This can be checked by ensuring the function passes the horizontal line test.
What are some real-world applications of inverse functions?
+Inverse functions have applications in physics, engineering, economics, and data analysis. They can be used to model supply and demand curves, solve triangles, and understand complex relationships between variables.
Meta Description: Learn how to find the inverse of a function with step-by-step instructions, examples, and applications in mathematics and real-world scenarios. Master the concept of inverse functions to deepen your understanding of mathematical relationships and solve complex problems.



