Major Semi Axis
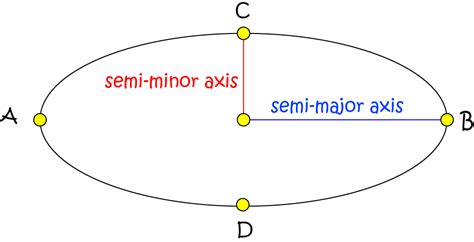
The major semi-axis, also known as the semi-major axis, is a fundamental concept in astronomy and astrodynamics. It refers to the longest radius of an elliptical orbit, which is a crucial parameter in describing the shape and size of the orbit. In this article, we will delve into the details of the major semi-axis, its significance, and its applications in various fields.
To understand the major semi-axis, it's essential to familiarize ourselves with the basics of elliptical orbits. An elliptical orbit is a closed curve that an object follows as it revolves around a central body, such as a planet or a star. The shape of the orbit is defined by its semi-major axis (a), semi-minor axis (b), and eccentricity (e). The semi-major axis is the average distance of the object from the central body, while the semi-minor axis is the shortest radius of the orbit. The eccentricity, which ranges from 0 to 1, determines the degree of ellipticity, with 0 representing a perfect circle and 1 representing a parabolic trajectory.
Key Points
- The major semi-axis is the longest radius of an elliptical orbit.
- It is a critical parameter in describing the shape and size of an orbit.
- The semi-major axis is related to the orbital period and the mass of the central body.
- Understanding the major semi-axis is essential in various fields, including astronomy, astrodynamics, and space exploration.
- Calculating the semi-major axis requires knowledge of the orbital parameters, such as the eccentricity, inclination, and longitude of the ascending node.
Orbital Parameters and the Major Semi-Axis

The major semi-axis is closely related to other orbital parameters, such as the orbital period (T), the mass of the central body (M), and the gravitational constant (G). According to Kepler’s third law, the square of the orbital period is proportional to the cube of the semi-major axis. This relationship is expressed as T^2 = (4π^2/G * M) * a^3, where a is the semi-major axis. This equation highlights the significance of the major semi-axis in determining the orbital period and the overall dynamics of the system.
Calculating the Semi-Major Axis
Calculating the semi-major axis requires knowledge of the orbital parameters, such as the eccentricity, inclination, and longitude of the ascending node. The semi-major axis can be calculated using the vis-viva equation, which relates the velocity of the object to its distance from the central body. The vis-viva equation is given by v^2 = G * M * (2/r - 1/a), where v is the velocity, r is the distance from the central body, and a is the semi-major axis. By rearranging this equation, we can solve for the semi-major axis, which is essential in determining the shape and size of the orbit.
| Orbital Parameter | Symbol | Unit |
|---|---|---|
| Semi-major axis | a | meters (m) |
| Eccentricity | e | unitless |
| Orbital period | T | seconds (s) |
| Mass of central body | M | kilograms (kg) |
| Gravitational constant | G | m^3 kg^-1 s^-2 |

Applications of the Major Semi-Axis

The major semi-axis has numerous applications in various fields, including astronomy, astrodynamics, and space exploration. In astronomy, the semi-major axis is used to determine the distance of celestial bodies from the central body, such as the Sun or a planet. This information is essential in understanding the dynamics of the solar system and the behavior of celestial bodies. In astrodynamics, the semi-major axis is used to calculate the orbital parameters of spacecraft and satellites, which is critical in designing and executing space missions. In space exploration, the semi-major axis is used to determine the trajectory of spacecraft and predict their motion, which is essential in ensuring the success of space missions.
In addition to its applications in astronomy and space exploration, the major semi-axis also has implications in other fields, such as geophysics and climate science. For example, the semi-major axis of the Earth's orbit around the Sun affects the amount of solar energy the planet receives, which in turn affects the climate. Understanding the major semi-axis is therefore essential in modeling the Earth's climate and predicting future climate changes.
What is the significance of the major semi-axis in astronomy?
+The major semi-axis is significant in astronomy because it determines the shape and size of an orbit, which is essential in understanding the dynamics of the solar system and the behavior of celestial bodies.
How is the semi-major axis related to the orbital period?
+The semi-major axis is related to the orbital period through Kepler's third law, which states that the square of the orbital period is proportional to the cube of the semi-major axis.
What are the applications of the major semi-axis in space exploration?
+The major semi-axis has numerous applications in space exploration, including determining the trajectory of spacecraft and predicting their motion, which is essential in ensuring the success of space missions.
In conclusion, the major semi-axis is a fundamental concept in astronomy and astrodynamics, and its understanding is essential in various fields, including space exploration and climate science. By calculating the semi-major axis, scientists and engineers can determine the shape and size of an orbit, which is critical in predicting the motion of celestial bodies and designing space missions. As our understanding of the universe continues to evolve, the significance of the major semi-axis will only continue to grow, and its applications will expand into new and exciting areas of research and exploration.



