Ml To Cm3

The conversion from milliliters (mL) to cubic centimeters (cm³) is a fundamental concept in the realm of measurement, particularly in scientific and medical fields. Understanding this conversion is crucial for accurate calculations and applications. In this article, we will delve into the details of this conversion, exploring the principles behind it, the conversion factor, and practical examples to illustrate its application.
Understanding Milliliters and Cubic Centimeters

Milliliters (mL) and cubic centimeters (cm³) are units of volume in the metric system. A milliliter is one-thousandth of a liter, and a cubic centimeter is the volume of a cube with sides of one centimeter. Both units are used to measure the volume of liquids, gases, and solids, but they are often used in different contexts due to their relationship.
The Conversion Factor
The conversion from milliliters to cubic centimeters is based on the fact that 1 milliliter is equal to 1 cubic centimeter. This means that the conversion factor between mL and cm³ is 1:1. To convert a volume in milliliters to cubic centimeters, you simply use the equation: volume in cm³ = volume in mL. This straightforward relationship simplifies many calculations, especially in laboratory settings where precise volume measurements are critical.
| Unit | Conversion to Cubic Centimeters |
|---|---|
| 1 milliliter (mL) | = 1 cubic centimeter (cm³) |
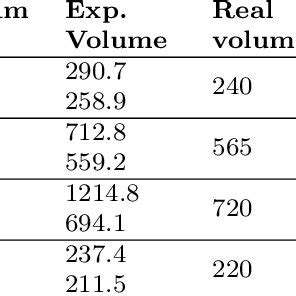
Practical Applications and Examples

The conversion between milliliters and cubic centimeters has numerous practical applications. For instance, in medical settings, dosages of medications are often given in milliliters, while the volume of bodily fluids might be measured in cubic centimeters. Understanding the equivalence can help in calculating the appropriate dosages or in interpreting medical test results.
Calculations and Conversions
To demonstrate the application of this conversion, let’s consider an example. Suppose you need to convert 500 mL of a solution to cubic centimeters. Given the 1:1 conversion factor, 500 mL is equal to 500 cm³. This calculation is straightforward and highlights the simplicity of converting between these two units.
Another example involves converting a larger volume, such as 2,000 mL, to cubic centimeters. Using the same conversion factor, 2,000 mL equals 2,000 cm³. This equivalence is useful in a variety of applications, from cooking and food preparation to industrial manufacturing processes.
Key Points
- The conversion from milliliters (mL) to cubic centimeters (cm³) is 1:1.
- 1 milliliter is equal to 1 cubic centimeter.
- This conversion is crucial in scientific, medical, and industrial applications.
- Understanding the equivalence can help in avoiding measurement errors and in facilitating calculations.
- The conversion applies to all contexts where volume measurements are necessary.
Conclusion and Future Directions
In conclusion, the conversion from milliliters to cubic centimeters is a fundamental concept that underlies many scientific and practical applications. The 1:1 conversion factor simplifies calculations and facilitates accurate volume measurements across different fields. As technology and scientific research continue to advance, the importance of precise measurements and conversions will only grow, making this basic principle a cornerstone of future developments.
What is the conversion factor between milliliters and cubic centimeters?
+The conversion factor is 1:1, meaning 1 milliliter equals 1 cubic centimeter.
Why is understanding the conversion between mL and cm³ important?
+It is crucial for accurate calculations and measurements in various fields, including science, medicine, and industry, helping to avoid errors and ensure precision.
Are there any differences in the application of mL and cm³ in practice?
+While the units are equivalent, the choice between milliliters and cubic centimeters may depend on the context or convention within a specific field or application.
Meta Description: Learn about the conversion from milliliters (mL) to cubic centimeters (cm³), including the conversion factor, practical applications, and examples to facilitate accurate volume measurements in science, medicine, and industry.



