Positively Skewed Vs Negatively Skewed
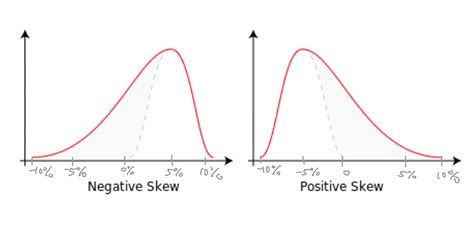
The concept of skewness is a fundamental aspect of statistics and data analysis, referring to the asymmetry of the probability distribution of a real-valued random variable. In essence, skewness describes how the distribution of data deviates from being perfectly symmetrical. There are three types of skewness: positively skewed, negatively skewed, and symmetrical. Understanding the differences between positively skewed and negatively skewed distributions is crucial for accurate data interpretation and decision-making in various fields, including finance, economics, and social sciences.
Key Points
- Skewness refers to the asymmetry of a probability distribution, indicating how it deviates from symmetry.
- A positively skewed distribution has a long tail on the right side, meaning extreme values are more likely to occur on the higher end.
- A negatively skewed distribution has a long tail on the left side, indicating that extreme values are more likely to occur on the lower end.
- The mode is typically the highest peak in a distribution, and in skewed distributions, it does not coincide with the mean or median.
- Understanding skewness is essential for statistical analysis, as it affects the choice of statistical measures and interpretations.
Positively Skewed Distribution
A positively skewed distribution, also known as a right-skewed distribution, is characterized by a long tail extending towards the right side of the distribution curve. This means that the majority of the data points are concentrated on the left side of the distribution, with fewer data points scattered towards the right. In a positively skewed distribution, the mean is typically greater than the median, which is greater than the mode. This type of distribution is common in datasets where there are extreme values on the higher end, such as income levels in a population where a small number of individuals have significantly higher incomes than the rest.
Characteristics of Positively Skewed Distributions
Positively skewed distributions exhibit several key characteristics: - The mean is pulled towards the tail of the distribution, making it less representative of the typical value. - The median is often a better representation of the central tendency than the mean in positively skewed distributions. - The mode, the value that appears most frequently, is usually on the left side of the distribution, away from the tail. - Statistical measures such as the standard deviation may not fully capture the variability in the data due to the presence of extreme values.
| Statistic | Positively Skewed |
|---|---|
| Mean | Greater than Median |
| Median | Greater than Mode |
| Mode | Typically the smallest value of the three |

Negatively Skewed Distribution
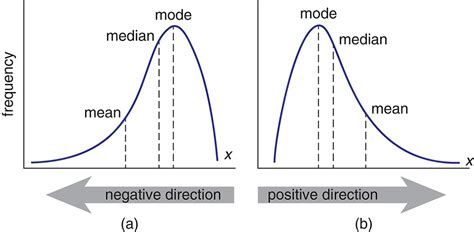
A negatively skewed distribution, or left-skewed distribution, has a long tail extending towards the left side of the distribution curve. This indicates that the majority of the data points are concentrated on the right side of the distribution, with fewer data points scattered towards the left. In a negatively skewed distribution, the mean is typically less than the median, which is less than the mode. This type of distribution can be seen in datasets where there are extreme values on the lower end, such as test scores where a few students score significantly lower than the rest.
Characteristics of Negatively Skewed Distributions
Negatively skewed distributions have the following characteristics: - The mean is pulled towards the lower end of the distribution, making it less representative of the typical value. - The median is often more representative of the central tendency than the mean in negatively skewed distributions. - The mode is usually on the right side of the distribution, away from the tail. - Similar to positively skewed distributions, statistical measures may not fully capture the data’s variability due to extreme lower values.
Implications of Skewness
The skewness of a distribution has significant implications for data analysis and interpretation. It affects the choice of statistical measures and the interpretation of results. For instance, in a positively skewed distribution, the mean may overestimate the typical value due to the influence of extreme high values, whereas in a negatively skewed distribution, the mean may underestimate the typical value due to the influence of extreme low values. Therefore, understanding whether a distribution is positively or negatively skewed is essential for applying appropriate statistical techniques and for drawing valid conclusions from the data.
Dealing with Skewed Distributions
When dealing with skewed distributions, several strategies can be employed: - Transformation of data: Applying transformations such as logarithmic or square root can help normalize the distribution, making it more symmetrical. - Use of robust statistical methods: Methods that are less sensitive to outliers, such as the median and interquartile range, can provide a more accurate representation of the data. - Truncation or winsorization: Reducing the impact of extreme values by truncating the data at a certain point or replacing a portion of the data at the extremes with a less extreme value can help in some analyses.
What is the primary difference between a positively and negatively skewed distribution?
+The primary difference lies in the direction of the tail. A positively skewed distribution has a long tail on the right, indicating extreme values are more likely on the higher end, whereas a negatively skewed distribution has a long tail on the left, indicating extreme values are more likely on the lower end.
How does skewness affect statistical analysis?
+Skewness affects the choice of statistical measures and the interpretation of results. It can make the mean less representative of the typical value and may require the use of alternative measures such as the median or the application of data transformations to normalize the distribution.
What strategies can be used to deal with skewed distributions?
+Strategies include transforming the data to make it more symmetrical, using robust statistical methods that are less sensitive to outliers, and truncation or winsorization to reduce the impact of extreme values.
In conclusion, understanding the concept of skewness and being able to distinguish between positively and negatively skewed distributions is vital for accurate data analysis and interpretation. By recognizing the characteristics of each type of skewness and applying appropriate statistical strategies, analysts can draw more valid conclusions from their data, ultimately leading to better decision-making in various fields.



