Upside Down U In Math
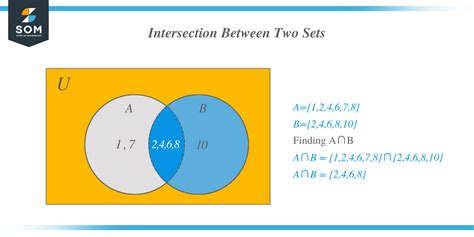
The upside-down U in math, also known as the union symbol, is denoted by the symbol ∪. It is used to represent the union of two or more sets, which is a fundamental concept in set theory. The union of two sets A and B, denoted by A ∪ B, is the set of all elements that are in A or in B or in both. This means that the union of two sets includes all the elements from both sets, without duplicates.
Definition and Notation

The union of two sets A and B is defined as the set of all elements x such that x is in A or x is in B. This can be written in mathematical notation as A ∪ B = {x | x ∈ A or x ∈ B}. The symbol ∪ is used to denote the union operation, and it is read as “union” or “cup”. For example, if A = {1, 2, 3} and B = {3, 4, 5}, then A ∪ B = {1, 2, 3, 4, 5}.
Properties of Union
The union operation has several important properties, including:
- Commutativity: The order of the sets does not matter, i.e., A ∪ B = B ∪ A.
- Associativity: The union of three sets can be performed in any order, i.e., (A ∪ B) ∪ C = A ∪ (B ∪ C).
- Distributivity: The union of a set and the intersection of two sets is equal to the intersection of the union of the set and each of the two sets, i.e., A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C).
| Set Operation | Definition | Example |
|---|---|---|
| Union | A ∪ B = {x | x ∈ A or x ∈ B} | A = {1, 2, 3}, B = {3, 4, 5}, A ∪ B = {1, 2, 3, 4, 5} |
| Intersection | A ∩ B = {x | x ∈ A and x ∈ B} | A = {1, 2, 3}, B = {3, 4, 5}, A ∩ B = {3} |
| Complement | A' = {x | x ∉ A} | A = {1, 2, 3}, A' = {4, 5, 6,...} |

Applications of Union

The union operation has many applications in various fields, including:
- Database Systems: The union operation is used to combine the results of two or more queries.
- Computer Networks: The union operation is used to combine the sets of nodes or edges in a network.
- Statistics: The union operation is used to combine the sets of data points or samples.
Key Points
- The union of two sets A and B is the set of all elements that are in A or in B or in both.
- The union operation is denoted by the symbol ∪ and is read as "union" or "cup".
- The union operation has several important properties, including commutativity, associativity, and distributivity.
- The union operation has many applications in various fields, including database systems, computer networks, and statistics.
- Understanding the properties of union is essential for working with sets and performing set operations.
Conclusion and Future Directions
In conclusion, the upside-down U in math, also known as the union symbol, is a fundamental concept in set theory. The union operation has many applications in various fields, and understanding its properties is essential for working with sets and performing set operations. As mathematics and computer science continue to evolve, the union operation will remain a crucial tool for solving complex problems and analyzing large datasets.
What is the union of two sets?
+The union of two sets A and B is the set of all elements that are in A or in B or in both.
What are the properties of the union operation?
+The union operation has several important properties, including commutativity, associativity, and distributivity.
What are the applications of the union operation?
+The union operation has many applications in various fields, including database systems, computer networks, and statistics.
Meta Description: Learn about the upside-down U in math, also known as the union symbol, and its applications in set theory, database systems, and computer networks. Understand the properties of union and how it is used to combine sets.